Algorithm Spring semester
Table of contents:
- Algorithm
- Characteristics
- Need for analysis of algorithm
- Design strategis
- Pros and Cons of divide and conquer
- Application of Divide and Conquer Approach
- Data Structure
- Big O Notation
- Big Omega Notation
- Big Theta Notation
- Selection Sort
- Selection sort in python
Algorithm
Defn :
step by step procedure,every procedure have many instructions,every instruction have many logical instruction and every instruction goes to output
Characteristics:
- Deterministic
- It is known , what is the goal of the algorithm
- Termination
- An algorithm must be terminated
- input
- output
Need for Analysis of Algorithm
- Analysis of algorithm is the process of analyzing the problem sovling capabilities depends on time and space
- worst case
- maximum number of steps
- Best case
- minimum number of steps
- Average case
- Average number of steps
- worst case
Design Strategies
- Many algorithm are recursive in nature to solve a given problem recursively to dealing with sub-problems
-
In divide and conquer approach , a problem is divided into smaller problems,then the smaller problems are solved independently and finally smaller problems are combined into a solution for the large problem
Generally divide and conquer algorithms have 3 parts
- Divde the problem into a number of sub-problems
- Conquer the sub-problems by solving them recursively
- Combine the solution to the sub-problem into the solution for the original problem
Pros and Cons of Divide and Conquer
- An algorithm which is designed using this technique, can run on the multiprocessor system or in different machines simultaneously
- In this approach, most of the algorithms are designed using recursion,hence memory management is very high
- For recursive function stack is used, where function state needs to be stored
Application of Divide and Conquer Approach
- Following are some problems, which are solved using divide and conquer approach
- Finding the maximum and minimum of a sequence of numbers
- Matrix Multiplication
- Merge Sort
- Binary Search
Data Structure:
A way to store , organise and manipulate data within a computer, in an efficient manner
Asymptotic Notation: 3 types:-
1. Big oh - O()
2. Big omega - Ω()
3. Big theta - Θ()
Big Oh Notation:
If ∃ (there exists or there is at least one) constants a,k > 0 such f(n) ≤ a * g(n) and ∀ n ≥ k, then f(n) = O(g(n))
- Upper bound on the order of growth of a function
Graphical Representation:
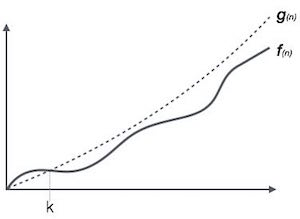
Example:
f(n) = 20n3 + 5n2 + 3
g(n) = n3
Is it f(n) = O(g(n))?
Solution:
we know, If ∃ (there exists or there is at least one) constants a,k > 0 such f(n) ≤ a * g(n) and ∀ n ≥ k, then f(n) = O(g(n)) so, we get,
20n3 + 5n2 + 3 ≤ 20n3 + 5n3 + 3n3
or, 20n3 + 5n2 + 3 ≤ 28n3
so, a = 28 and b = 1 and all other conditions a * g(n) satisfied
Big Omega Notation
If ∃ (there exists or there is at least one) constants a,k > 0 such f(n) ≥ a * g(n) and ∀ n ≥ k, then f(n) = Ω(g(n))
Graphical View:
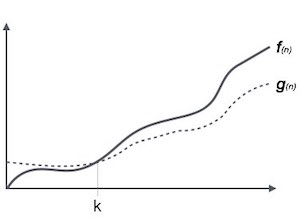
Big Theta Notation
If ∃ (there exists or there is at least one) constants a1,a2,k > 0 such that a 1 x g(n) ≤f(n) ≤ a 2 x g(n) and ∀ n ≥ k, then f(n) = Θ(g(n))
Graphical View:
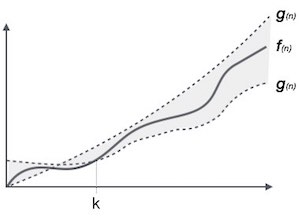
Example:
f(n) = n2 + 2 g(n) = n2 Is that , f(n) = Θ(g(n))?
Solution:
If ∃ (there exists or there is at least one) constants a1,a2,k > 0 such that a 1 x g(n) ≤f(n) ≤ a 2 x g(n) and ∀ n ≥ k, then f(n) = Θ(g(n))
1 * n 2 ≤ n 2 + 2 ≤ 2 + n 2
so, a1 ,a2 = 2 and b = 1
and all other condition satisfied
so, we can say, f(n)= Θ(g(n))
Selection Sort
- In this technique, we find the smallest-element and place it in the appropirate position
- If we have n elements then it requires (n-1) pass to sort the elements
Array
| index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| elements | 3 | 7 | 6 | 2 | 1 |
Here, we have 5 elements . so we need (5-1) = 4 pass to sort the array
Pass1:
In pass1 smallest element is searched between A[0] to A[4] and swapped with A[0]
| index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| elements | 3 | 7 | 6 | 2 | 1 |
![]()
| index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| elements | 1 | 7 | 6 | 2 | 3 |
Pass2:
In pass 2 smallest element is searched between A[1] to A[4] and swapped with A[1]
| index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| elements | 1 | 2 | 6 | 7 | 3 |
Pass3:
In pass 3 smallest element is searched between A[2] to A[4] and swapped with A[2]
| index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| elements | 1 | 2 | 3 | 7 | 6 |
Pass4:
In pass 4 smallest element is searched between A[3] to A[4] and swapped with A[3]
| index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| elements | 1 | 2 | 3 | 6 | 7 |
Selection Sort in python
# Array elements
A = [ 3,7,6,2,1]
# Traverse through all array elements
for i in range(len(A)):
# let mimimum value of index
minimum = i
# find the minimum element in unsorted array
for j in range(i+1,len(A)):
if A[minimum] > A[j]:
minimum = j
# swap the minimum element with first elment
A[i], A[minimum] = A[minimum], A[i]
#Print sorted array
print("Sorted Array:")
for i in range(len(A)):
print("%d" %A[i]),
Sorted Array:
1
2
3
6
7
Space Complexity
Analysis of space complexity of an algorithm or program is the ? amout of memory it needs to run to completion some of the reasons for swapping
space complexity are:
- Swapping without third variable
- longest number finding with ternary operator
-
If the program is to run variable on multiuser system,it may be required to specify the amount of memory to be allocated to program
-
To Know in advance that sufficient memory is available to run the program
-
Can be used to estimate the size of the largest problem that a program can solve.
Merge Sort Algorithm
Merge(A,p,n,q,r)
n1 = q-p+1
n2 = r-q
Let L(1....n1 + 1) and R(1 to n2+1) be new arrays
for ( i = 1 to n1)
L[i] = A[p+i-1]
for(j=1 to n2)
R[j] = A[q+j]
L[n1+1] = infinity
R[n2+1] = infinity
i = 1
j = 1
for(k=p to r)
if(L[i] <= R[j])
A[k] = L[i]
i+=1
else
A[k] = R[j]
j += 1
explanation


Knapsack Problem
Given, total knapsack weight = 16
Array of weight = 16
Array of weight (w1,w2,w3,w4,w5,w6) = (1,3,5,6,3,10)
Array of Profit (p1,p2,p3,p4,p5,p6) = (3,5,8,6,1,2)
| Item | weight,wi | Profit,pi | Density, Pi / wi |
|---|---|---|---|
| I5 | 1 | 3 | 3.00 |
| I6 | 3 | 5 | 1.67 |
| I4 | 5 | 8 | 1.60 |
| I1 | 6 | 6 | 1.00 |
| I3 | 3 | 1 | 0.33 |
| I2 | 2 | 2 | 0.20 |
Knapsack Solution
| Item | weight | Profit | Commutative weight | Benefit |
|---|---|---|---|---|
| I5 | 1 | 3 | 1 | 3 |
| I6 | 3 | 5 | 4 | 8 |
| I4 | 5 | 8 | 9 | 16 |
| I1 | 6 | 6 | 15 | 22 |
| I3 | 1 | 0.33 | 16 | 22.33 |
Binary Search Algorithm
Binary(data, lb, ub, item, loc)
[Here ,data is a sorted array, where lower bound is ‘LB’,upper bound =’UB’,item = identified data element]
Beg, End, Mid 3 variables => where beg = 1st segment, end = end segment and mid = Middle segment of array element
- beg := LB, end := UB , and Mid := Int( ( beg + end ) / 2 )
- beg <= end and data[mid] != item
- repeat step 3 and 4
-
If item < data[mid]
end = mid -1
else
beg = mid + 1
- Mid := Int( ( beg / end ) / 2 )
-
If data[mid] = item
loc = mid
else
loc = null
Bubble Sort
let data elements A[1] A[2] …. A[N]
step1:
Compare A[1] and A[2] if A[1] > A[2] then swapping
if A[1] < A[2] then no change,no swapping
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| elements | 32 | 51 | 27 | 85 | 66 | 23 | 13 | 57 |
Pass1:
- 32 < 51 , swap no
- 51 > 27 swapping
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| elements | 32 | 27 | 51 | 85 | 66 | 23 | 13 | 57 |
- 51 < 85 , now swap
- 85 > 66 , swapping
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| elements | 32 | 27 | 51 | 66 | 85 | 23 | 13 | 57 |
- 85 > 23 , swapping
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| elements | 32 | 27 | 51 | 66 | 23 | 85 | 13 | 57 |
- 85 > 13, swapping
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| elements | 32 | 27 | 51 | 66 | 23 | 13 | 85 | 57 |
- 85 > 57 , swapping
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| elements | 32 | 27 | 51 | 66 | 23 | 13 | 57 | 85 |
pass2 and others:
please try yourself
Algorithm Bubble sort
BubbleSort(A)
for i in range(1,length(A))
do for i length(A) down to i+1
do if A[j] < A[j-1]
then exchange A[j] <-> A[j-1]
Longest Increasing Subsequence
Given Sequence : 1 , 6, 2, 4, 5, 0
subsequence : (2) or (1,4) or(6,4,0)
Increasing Subsequence : ( 1,6),(1,2)(1,2,4)
Notice that (1),(6),(5) etc are also increasing subsequence
Increasing Sequence : (1),(6),(2),(4),(5),(0)
= (1,6),(1,2),(1,2,4),(1,2,4,5),(0)
LIS = 1 2 2 3 4 1
so answer = maxof(LIS) = 4